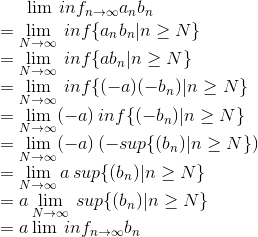Limes superior und Limes inferior von Mengenfolgen

In der Mathematik sind der Limes superior und der Limes inferior einer Mengenfolge Begriffe aus der Maßtheorie und Wahrscheinlichkeitstheorie, die die Begriffe des Limes superior und Limes inferior von Zahlenfolgen und Funktionenfolgen für Mengenfolgen verallgemeinern. Sie dienen beispielsweise in der Stochastik zur Modellierung von Ereignissen, die unendlich oft auftreten oder zur Definition von konvergenten Mengenfolgen. Der Begriff geht auf Émile Borel zurück.

Definition

Gegeben sei eine Mengenfolge ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ in der Obermenge ${\displaystyle \Omega }$. Dann heißt

${\displaystyle \liminf _{n\rightarrow \infty }A_{n}={\bigcup _{n=1}^{\infty }}\left({\bigcap _{m=n}^{\infty }}A_{m}\right)}$

der Limes inferior der Mengenfolge und

${\displaystyle \limsup _{n\rightarrow \infty }A_{n}={\bigcap _{n=1}^{\infty }}\left({\bigcup _{m=n}^{\infty }}A_{m}\right)}$

der Limes superior der Mengenfolge. Alternative Schreibweisen sind ${\displaystyle \varliminf _{n\to \infty }}$ für den Limes inferior oder ${\displaystyle \varlimsup _{n\to \infty }}$ für den Limes superior.

Beispiel

Betrachte als Beispiel die Mengenfolge ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ mit

${\displaystyle A_{n}:=[-1,n]}$

auf der Grundmenge ${\displaystyle \Omega =\mathbb {R} }$. Es ist nun

${\displaystyle B_{n}:=\bigcap _{m=n}^{\infty }A_{m}=[-1,n]}$.

Daraus folgt direkt

${\displaystyle \liminf _{n\rightarrow \infty }A_{n}=\bigcup _{n=1}^{\infty }B_{n}=\bigcup _{n=1}^{\infty }[-1,n]=[-1,\infty ).}$

Analog folgt für den Limes superior

${\displaystyle C_{n}:=\bigcup _{m=n}^{\infty }A_{m}=[-1,\infty )}$

und damit

${\displaystyle \limsup _{n\rightarrow \infty }A_{n}=\bigcap _{n=1}^{\infty }C_{n}=\bigcap _{n=1}^{\infty }[-1,\infty )=[-1,\infty ).}$

Interpretation

Der Limes superior und inferior lässt sich wie folgt interpretieren:

${\displaystyle \limsup _{n\to \infty }A_{n}=\{\omega \in \Omega \,|\,\omega {\text{ ist in unendlich vielen der Mengen }}A_{n}{\text{ enthalten }}\}}$

${\displaystyle \liminf _{n\to \infty }A_{n}=\{\omega \in \Omega \,|\,\omega {\text{ ist in allen bis auf endlich viele der Mengen }}A_{n}{\text{ enthalten }}\}}$

Man kann sich dies an den Formeln klarmachen, wenn man die äußere Mengenoperation ausschreibt. Es ist dann

${\displaystyle \liminf _{n\to \infty }A_{n}={\bigcap _{m=1}^{\infty }}A_{m}\cup {\bigcap _{m=2}^{\infty }}A_{m}\cup {\bigcap _{m=3}^{\infty }}A_{m}\dots }$

Dabei ist jede der Mengen ausgeschrieben

${\displaystyle C_{N}:={\bigcap _{m=N}^{\infty }}A_{m}=\{\omega \in \Omega \,|\,\omega \in A_{n}{\text{ für alle }}n\geq N\}}$.

Vereinigt man nun alle der ${\displaystyle C_{N}}$, um den Limes inferior zu bilden, so enthält die Vereinigungsmenge alle Elemente der Obermenge, die in mindestens einem ${\displaystyle C_{N}}$ enthalten sind. Dies ist äquivalent dazu, dass zu jedem Element ${\displaystyle \omega }$ ein Index ${\displaystyle N}$ existiert, so dass ${\displaystyle \omega }$ in jedem ${\displaystyle A_{n}}$ enthalten ist, wenn ${\displaystyle n\geq N}$ ist. Dies kann aber nur der Fall sein, wenn ${\displaystyle \omega }$ in allen bis auf endlich vielen ${\displaystyle A_{n}}$ enthalten ist, also nur endlich viele ${\displaystyle A_{n}}$ das Element nicht enthalten.

Analog ergibt sich für den Limes superior

${\displaystyle \limsup _{n\to \infty }A_{n}={\bigcup _{m=1}^{\infty }}A_{m}\cap {\bigcup _{m=2}^{\infty }}A_{m}\cap {\bigcup _{m=3}^{\infty }}A_{m}\dots }$

Dann sind die einzelnen Vereinigungsmengen

${\displaystyle D_{N}={\bigcup _{m=N}^{\infty }}A_{m}=\{\omega \in \Omega \,|\,{\text{ Es gibt ein }}n\geq N,{\text{ so dass }}\omega \in A_{n}{\text{ ist }}\}}$

Schneidet man nun alle ${\displaystyle D_{N}}$, um den Limes superior zu bilden, so enthält die Schnittmenge alle ${\displaystyle \omega }$, die in jedem ${\displaystyle D_{N}}$ liegen. Dies sind dann aber genau die Elemente, die in unendlich vielen ${\displaystyle A_{n}}$ liegen. Der Schluss lässt sich veranschaulichen mit der Aussage: es gibt keine Grenze N ab der das Element in keiner folgenden Menge mehr vorkommt.

Zusammenhang mit charakteristischen Funktionen

Die charakteristischen Funktionen des Limes inferior bzw. Limes superior von Mengen sind der punktweise Limes inferior bzw. Limes superior der charakteristischen Funktionen der einzelnen Mengen: Aus

${\displaystyle \chi _{A}(x)=\sup _{n}\chi _{A_{n}}(x)}$ für ${\displaystyle A=\bigcup _{n}A_{n}}$

und

${\displaystyle \chi _{A}(x)=\inf _{n}\chi _{A_{n}}(x)}$ für ${\displaystyle A=\bigcap _{n}A_{n}}$

folgt

${\displaystyle \chi _{\bigcup _{n}\bigcap _{m\geq n}A_{m}}(x)=\sup _{n}\chi _{\bigcap _{m\geq n}A_{m}}(x)=\sup _{n}\inf _{m\geq n}\chi _{A_{m}}(x),}$

analog für lim sup.

Insgesamt gilt also

${\displaystyle \chi _{\limsup \limits _{n\to \infty }A_{n}}=\limsup _{n\to \infty }\chi _{A_{n}}}$

und

${\displaystyle \chi _{\liminf \limits _{n\to \infty }A_{n}}=\liminf _{n\to \infty }\chi _{A_{n}}}$.

Verwendung

Der Limes superior von Mengenfolgen wird in der Wahrscheinlichkeitstheorie beispielsweise im Borel-Cantelli-Lemma oder im Kolmogorowschen Null-Eins-Gesetz verwendet, wo sie typische Beispiele von terminalen Ereignissen sind. Allgemeiner werden Limes superior und inferior dazu genutzt, um Konvergenz von Mengenfolgen zu definieren. Eine Mengenfolge konvergiert, wenn Limes inferior und superior übereinstimmen. Dies ist beispielsweise der Fall, wenn es zu jedem ${\displaystyle \omega }$ einen Index ${\displaystyle N=N(\omega )}$ gibt, so dass entweder ${\displaystyle \omega \in A_{n}}$ für alle ${\displaystyle n\geq N}$ oder ${\displaystyle \omega \notin A_{n}}$ für alle ${\displaystyle n\geq N}$ gilt. Konvergente Mengenfolgen treten beispielsweise in der Maßtheorie auf.

Literatur

• Jürgen Elstrodt: Maß- und Integrationstheorie. 6., korrigierte Auflage. Springer-Verlag, Berlin Heidelberg 2009, ISBN 978-3-540-89727-9, doi:10.1007/978-3-540-89728-6. 
• Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6.